LTPDA Toolbox™ contents System identification in z-domain   Fitting time series with polynomials

Generation of noise with given PSD

Generation of model noise is performed with the function ao/noisegen1D. Details on the algorithm can be found in noisegen1D help page.

Generation of noise with given PSD

During this exercise we will:

  1. Load from file an fsdata object with the model (obtained with a fit to the the PSD of test data with zDomainFit)
  2. Genarate noise from this model
  3. Compare PSD of the generated noise with original PSD

Let's open a new editor window and load the test data. 

    tn = ao(plist('filename', 'topic5/T5_Ex03_TestNoise.xml'));
    tn.setName();

This command will load an Analysis Object containing a test time series 10000 seconds long, sampled at 1 Hz. The command setName sets the name of the AO to be the same as the variable name, in this case tn.

Now let's calculate the PSD of our data. We apply some averaging, in order to decrease the fluctuations in the data. 

    tnxx = tn.psd(plist('Nfft', 2000));

Additionally, we load a smooth model that represents well our data. It was obtained, as described here, by fitting the target PSD with z-domain fitting. We load the data from disk, and plot them against the target PSD. Please note that the colouring filters (whose response represents our model) have no units, so we force them to be the same as the PSD we compare with: 

    fmod = ao(plist('filename', 'topic5/T5_Ex03_ModelNoise.xml'));
    iplot(tnxx, fmod.setYunits(tnxx.yunits))

The comparison beyween the target PSD and the model should look like:

We can now start the noise generation process. The first step is to generate a white time series Analysis Object, with the desired duration and units: 

    a = ao(plist('tsfcn', 'randn(size(t))', 'fs', 1, 'nsecs', 10000, 'yunits', 'm'));

Then we run the noise coloring process calling noisegen1D 

    plng = plist(...
          'model', fmod, ...      % model for colored noise psd
          'MaxIter', 50, ...      % maximum number of fit iteration per model order
          'PoleType', 2, ...      % generates complex poles distributed in the unitary circle
          'MinOrder', 20, ...     % minimum model order
          'MaxOrder', 50, ...     % maximum model order
          'Weights', 2, ...       % weight with 1/abs(model)
          'Plot', false, ...      % on to show the plot
          'Disp', false);         % on to display fit progress on the command window

    ac = noisegen1D(a, plng);

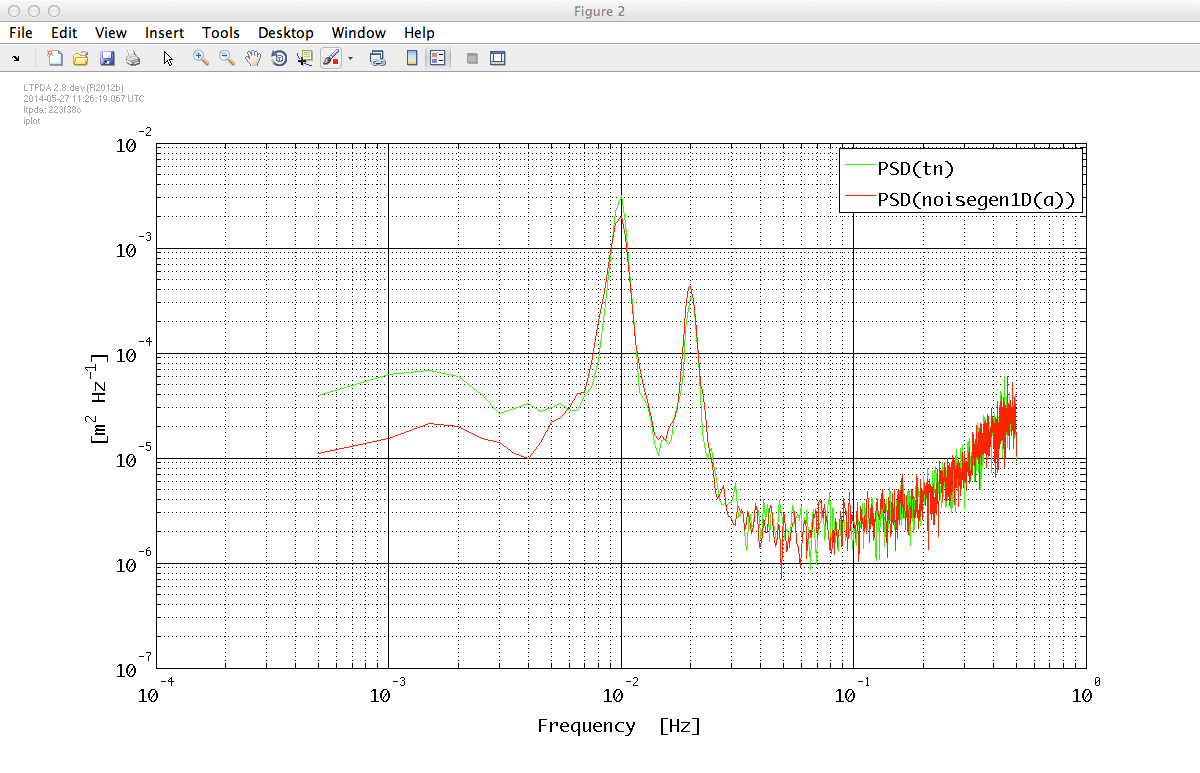
Let's check the result. We calculate the PSD of the generated noise and compare it with the PSD of the target data. 

    acxx = ac.psd(plist('Nfft', 2000));
    iplot(tnxx, acxx)

As can be seen, the result is in quite satisfactory agreement with the original data

Appendix: evaluation of the model for the noise PSD

The smooth model for the data, that we used to reproduce the synthesized noise, was actually obtained by applying the procedure of z-domain fitting that we discussed in the previous section. If you want to practise more with this fitting technique, we repost here the steps.

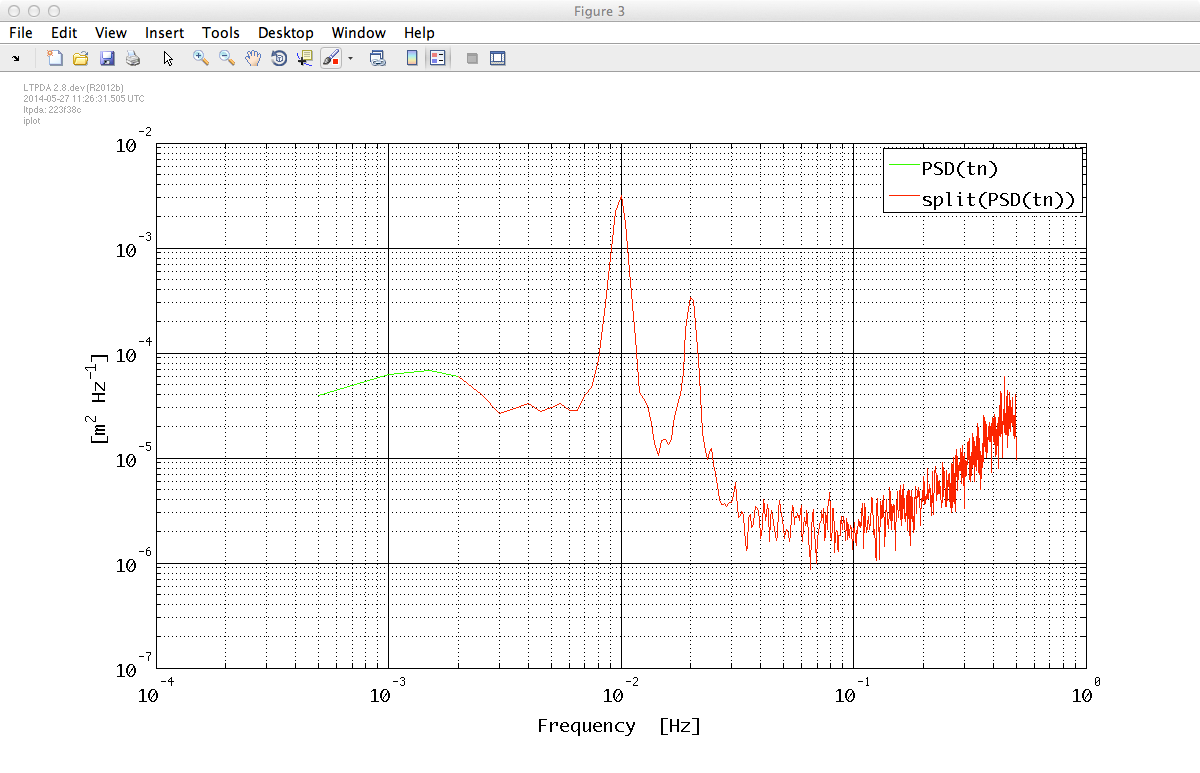
In order to extract a reliable model from PSD data we need to discard the first frequency bins; we do that by means of the split method. 

    tnxxr = split(tnxx, plist('frequencies', [2e-3 +inf]));
    iplot(tnxx, tnxxr)

The result should look like:

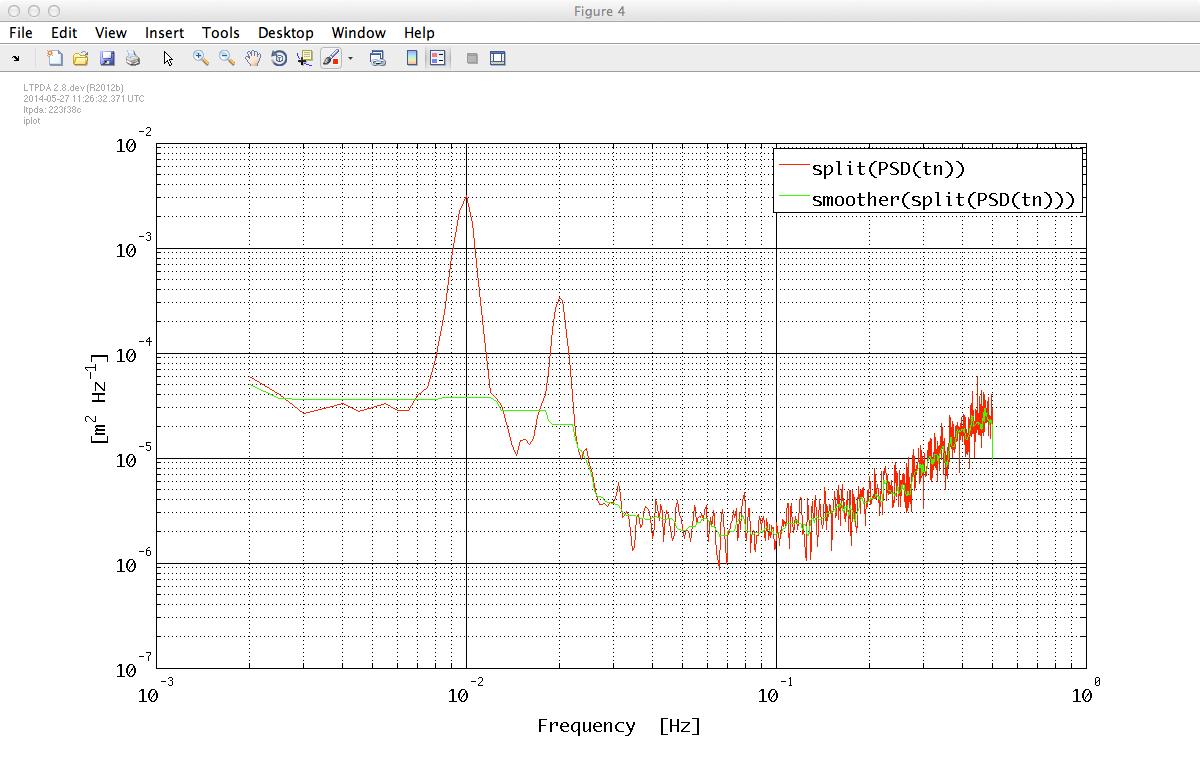
Now it's the moment to fit our PSD to extract a smooth model to pass to the noise generator. First of all we should define a set of proper weights for our fit process. We smooth our PSD data and then define the weights as the inverse of the absolute value of the smoothed PSD. This should help the fit function to do a good job with noisy data. It is worth noting here that weights are not univocally defined and there could be better ways to define them. 

    stnxx = smoother(tnxxr);
    iplot(tnxxr, stnxx)
    wgh = 1./abs(stnxx);

The result of the smoother method is shown in the plot below:

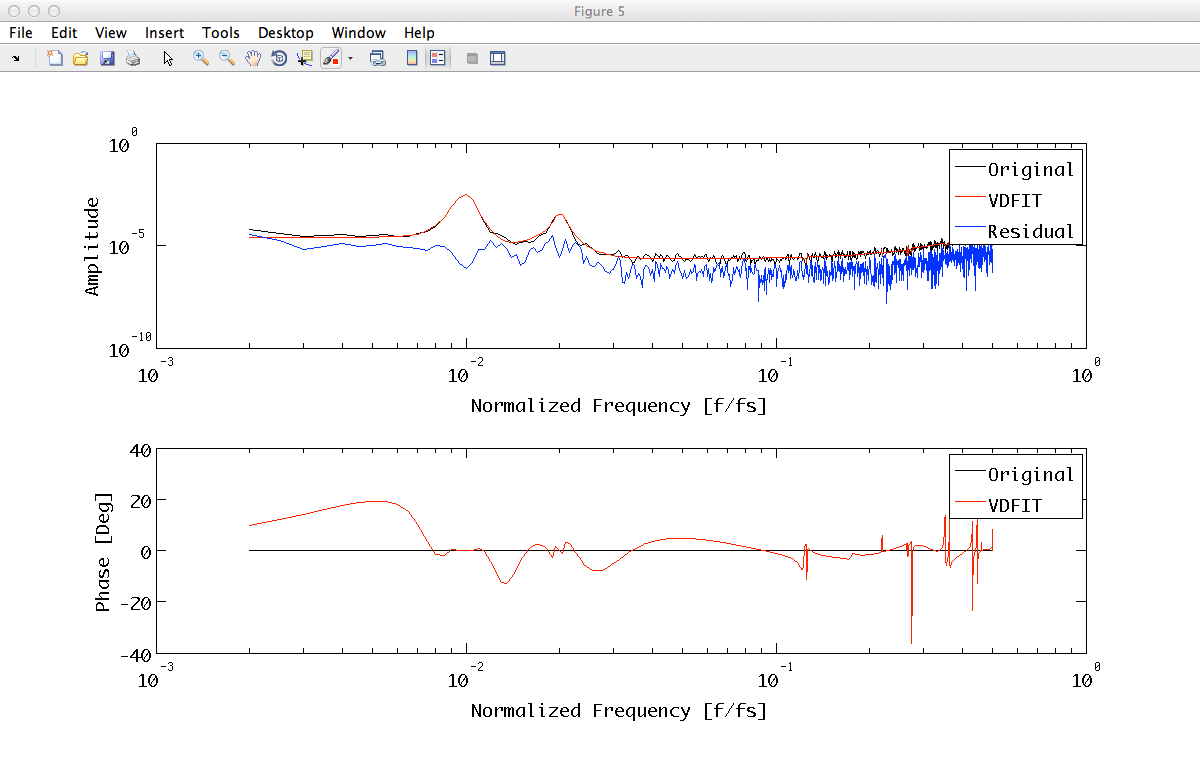
Now let's run an automatic search for the proper model and pass the set of externally defined weights. The first output of zDomainFit is a miir filter model; the second output is the model response. Note that we are setting 'ResFlat' parameter to define the exit condition. 'ResFlat' check the spectral flatness of the absolute value of the fit residuals. 

    plfit = plist('AutoSearch', 'on', ...
                  'StartPolesOpt','clog', ...
                  'maxiter', 50, ...
                  'minorder', 30, ...
                  'maxorder', 45, ...
                  'weights', wgh ,... % assign externally calculated weights
                  'condtype', 'MSE', ...
                  'msevartol', 0.1, ...
                  'fittol', 0.01, ...
                  'Plot', 'on', ...
                  'ForceStability', 'off', ...
                  'CheckProgress', 'off');

    % Do the fit
    fit_results = zDomainFit(tnxxr, plfit);

Fit result should look like:

The fit results consist in a filterbank object; we can evaluate the absolute values of the response of these filters at the frequencies defined by the x field of the PSD we want to match. 

% Evaluate the absolute value of the response of the colouring filter
b = resp(fit_results, plist('f', tnxxr.x));
b.abs;

% Save the model on disk
b.save(plist('filename', 'topic5/T5_Ex03_ModelNoise.xml'));


System identification in z-domain  System identification in z-domain   Fitting time series with polynomials Fitting time series with polynomials

©LTP Team