LTPDA Toolbox™ contents Fitting time series with polynomials   IFO/Temperature Example - signal subtraction

Non-linear least squares fitting of time series

Non-linear least square fitting of time-series exploits the function ao/xfit.

Non-linear least square fitting of time series

During this exercise we will:

  1. Load time series data
  2. Fit data with ao/xfit
  3. Check results
  4. Refine the fit with a Monte Carlo search

Let us open a new editor window and load test data. 

    a = ao(plist('filename', 'topic5/T5_Ex05_TestNoise.xml'));
    a.setName('data');
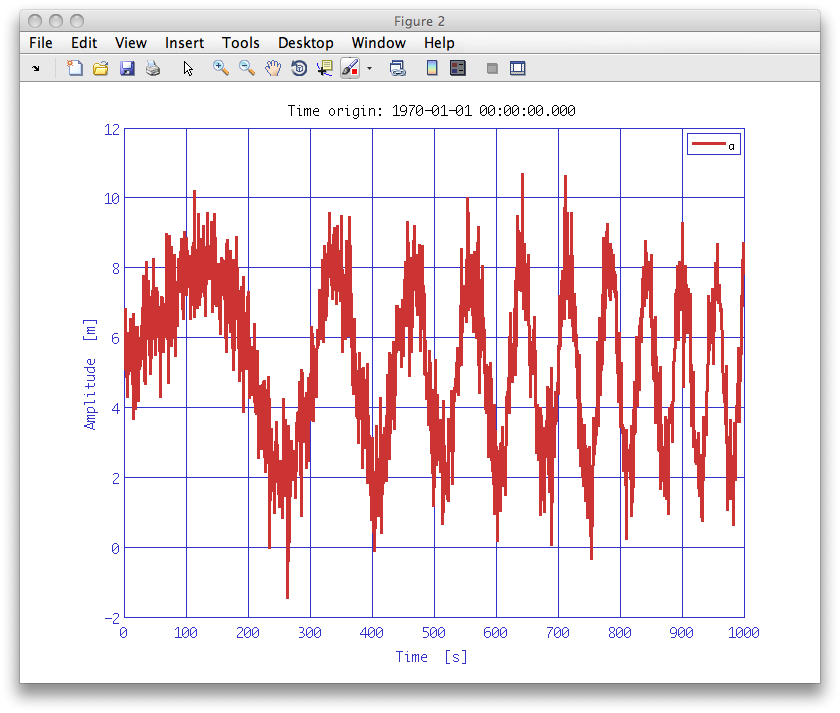
    iplot(a)

As can be seen this is a chirped sine wave with some noise.

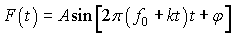
We could now try the fit. The first parameter to pass to xfit is a fit model. In this case we assume that we are dealing with a linearly chirped sine wave according to the equation:


The previous function can be stored within a smodel analysis object to pass to the fitting machinery: 
    mdl = smodel(plist('Name', 'chirp', ...
              'expression', 'A.*sin(2*pi*(f + f0.*t).*t + p) + c', ...
              'params', {'A', 'f', 'f0', 'p', 'c'}, ...
              'xvar', 't', ...
              'xunits', 's', 'yunits', 'm'));
We need to specify a starting guess for the model parameters. The output of ao/xfit is a pest analysis objects containing fit parameters. 

    plfit1 = plist('Function', mdl, ...
              'P0', [5, 9e-5, 9e-6, 0, 5]);

    params1 = xfit(a, plfit1);

Once the fit is done, we can evaluate our model to check fit results. 

    b = eval(params1, plist('xdata', a, 'xfield', 'x'));
    b.setName();    
    iplot(a, b)

As you can see, the fit is not accurate. One of the great problems of non-linear least square methods is that they easily find a local minimum of the chi square function and stop there without finding the global minimum. There are two possibile solutions to such kind of problems: the first one is to refine step by step the fit by looking at the data; the second one is to perform a Monte Carlo search in the parameter space. This way, the fitting machinery extracts the number of points you define in the 'Npoints' key, evaluates the chi square at those points, reoders by ascending chi square, selects the first guesses and fit starting from them. 

plfit2 = plist(...
		'Function', mdl, ...
		'MonteCarlo', 'yes', ...
		'Npoints', 1000, ...
		'LB', [1, 5e-5, 5e-6, 0, 2], ...
		'UB', [10, 5e-4, 5e-5, 2*pi, 7]);
    
    params2 = xfit(a, plfit2);
    
    c = eval(params2, plist('xdata', a, 'xfield', 'x'));
    c.setName();
    iplot(a, c)

The fit now looks like better...

Let us compare fit results with nominal parameters.
Data were generated with the following set of parameters: 

    A  = 3
    f  = 1e-4
    f0 = 1e-5
    p  = 0.3
    c  = 5

Fitted parameters are instead: 

    A  = 3.02 +/- 0.05
    f  = (7 +/- 3)e-5
    f0 = (1.003 +/- 0.003)e-5 
    p  = 0.33 +/- 0.04
    c  = 4.97 +/- 0.03

The correlation matrix of the parameters, the chi square, the degree of freedom, the covariance matrix are store in the output pest. Other useful information are stored in the procinfo (processing information) field. This field is a plist and is used to additional information that can be returned from algorithms. For example, to extract the chi square, we write: 

    params2.chi2
    1.0253740840052

And to know the correlation matrix: 

    params2.corr
    Columns 1 through 3

                         1         0.120986348157139       -0.0970894969803509
         0.120986348157139                         1        -0.966114904879414
       -0.0970894969803509        -0.966114904879414                         1
        -0.156801230958825        -0.848296014553159         0.717376893765734
       -0.0994358284166703         0.187645552903433        -0.169496082635319

    Columns 4 through 5

        -0.156801230958825       -0.0994358284166703
        -0.848296014553159         0.187645552903433
         0.717376893765734        -0.169496082635319
                         1        -0.199286767157984
        -0.199286767157984                         1

Not so bad!


Fitting time series with polynomials  Fitting time series with polynomials   IFO/Temperature Example - signal subtraction IFO/Temperature Example - signal subtraction

©LTP Team