Rational representation

Creating a rational model

Another possibility to build a transfer function model is to use the rational constructor, which implements a transfer function as a quotient of polynomials:

    
      % DESCRIPTION: RATIONAL rational representation of a transfer function.
      %
      %              a(1)s^m + a(2)s^{m-1} + ... + a(m+1)
      %      H(s) = --------------------------------------
      %              b(1)s^n + b(2)s^{n-1} + ... + b(n+1)
      %

For example if the numerator and denominator coefficients are given by:

num = [1 3 5]
den = [1 8 10]

then we need to write down the following

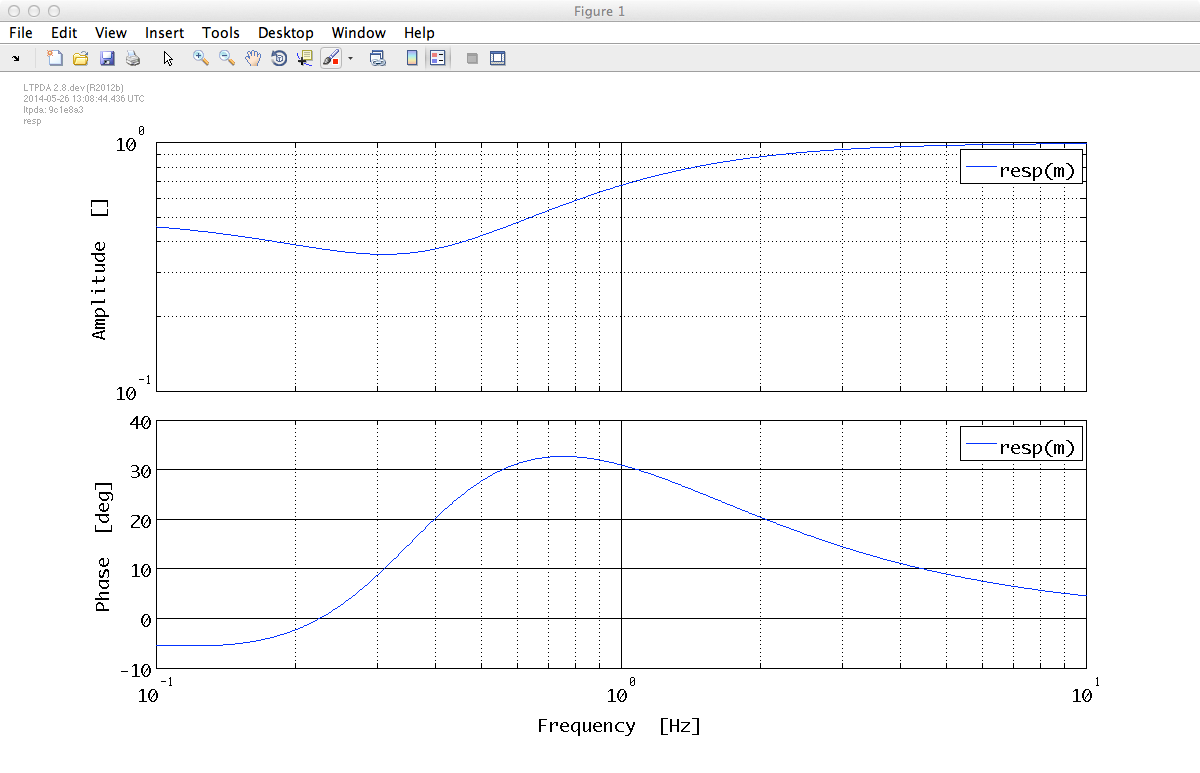
    m = rational([1 3 5], [1 8 10])

And now, as with the previous models, we can evaluate the response in a given frequency region

    resp(m, plist('f1', 0.1, 'f2', 10))

Response of a rational model

$Partial fraction representation$

Partial fraction representation

Transforming models between representations