

| LTPDA Toolbox™ | contents |   |
In this section we want to investigate how the DIST_* models behave, by simulating them. Let's begin with the DIST_CAPACT model, that provides the force/torque noise associated with the electrostatic actuation in the LPF TMs. We build the standard version of the system:
% Build the default version of the GRS CAPactive ACTuation noise model GRScapactNoise = ssm(plist('built-in', 'DIST_CAPACT'));
%% Get help on the GRS CAPactive ACTuation noise model
help ssm_model_DIST_CAPACT
%% Obtain more details about this model
GRScapactNoise.viewDetails
%% Calculate the bode response of the noise coloring filter for the continuous system, tm2_x port
tm2_xNoisePlist = plist(...
'inputs', 'DIST_CAPACT_NOISE.tm2_x', ...
'outputs', 'DIST_CAPACT.tm2_x', ...
'f', logspace(-4, log10(0.5), 1000) ... % from 0.1mHz to 0.5Hz
);
bode_out = bode(GRScapactNoise, tm2_xNoisePlist);
GRScapactNoise_tm2_x_cont_resp = bode_out.unpack();
| Remember: the output of bode is a matrix object. The single response we want (1 input to 1 output) is represented by the single ao inside the output matrix. So we unpack that single object from the matrix. |
In order to simulate the ssm models, we need to discretize them, by setting the time-step to a non-zero value.
%% Discretize the system to be simulated at 1 Hz
timestep = 1;
GRScapactNoise_discrete = GRScapactNoise.modifyTimeStep(timestep);%% Calculate the bode response of the noise coloring filter for the discrete system, tm2_x port bode_out = bode(GRScapactNoise_discrete, tm2_xNoisePlist); GRScapactNoise_tm2_x_disc_resp = bode_out.unpack(); %% Compare the transfer functions for the discrete and continuous case iplot(GRScapactNoise_tm2_x_cont_resp, GRScapactNoise_tm2_x_disc_resp);
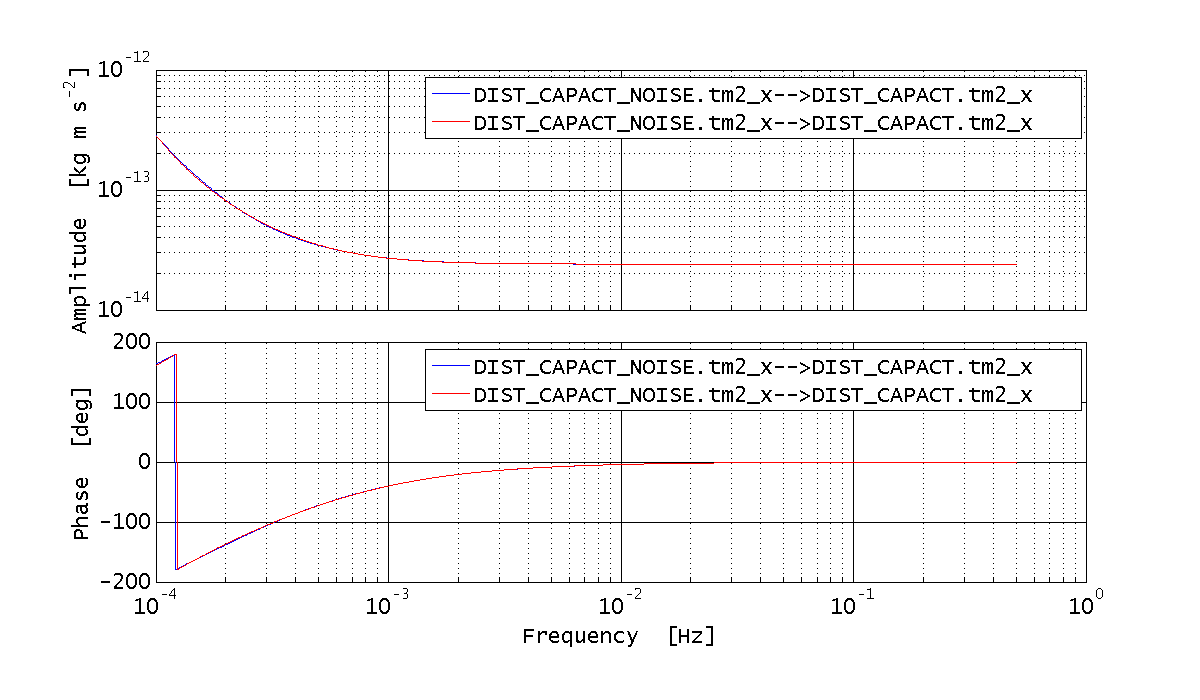
Let's assume we only want to simulate the effect of the force noise acting on TM2 along x, so we simulate a single noise source. We can do that by specifying a single input name and a value for the CPSD of that noise source:
%% Simulate the system behavior: only tm2_x force noise % Simulation configuration plist simPlist_noise = plist(... 'CPSD Variable Names', 'DIST_CAPACT_NOISE.tm2_x', ... 'CPSD', 1, ... 'Return outputs', {'DIST_CAPACT.tm2_x'}, ... 'Nsamples', 1e6 ... ); % Launch the simulation sim_output = GRScapactNoise_discrete.simulate(simPlist_noise); % Extract the AO with the force data out_tm2_x = sim_output.unpack(); % Plot the results iplot(out_tm2_x)
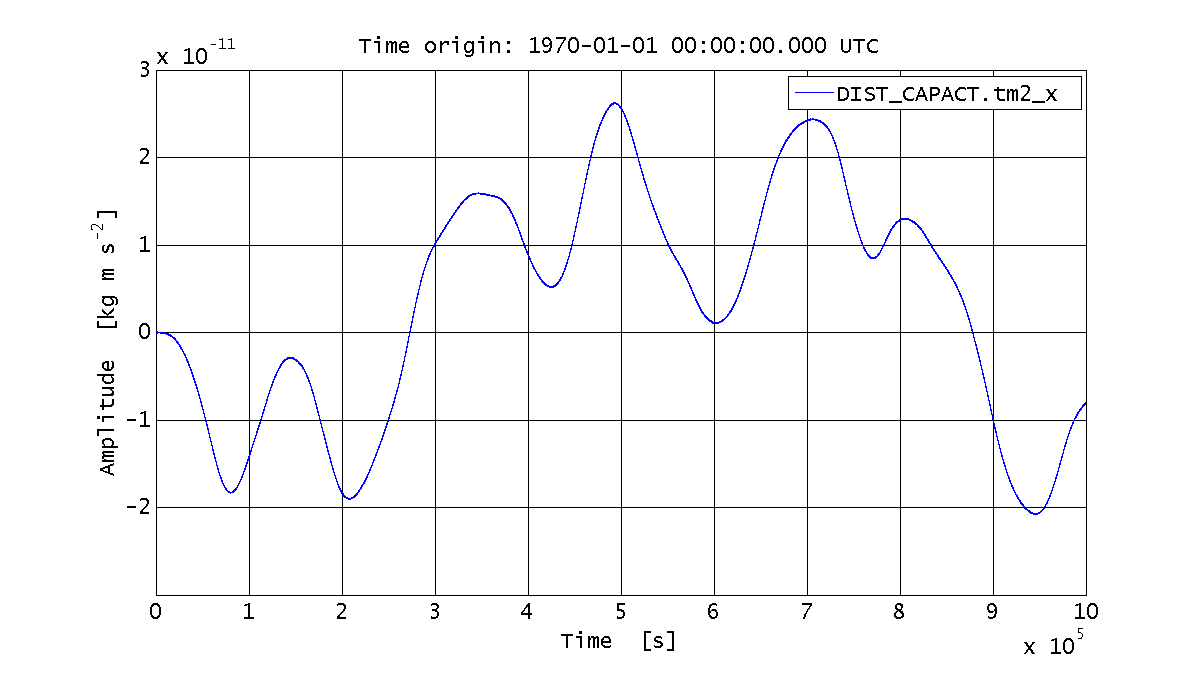
Eventually, we want to estimate the PSD of the force. We also want to compare the estimated PSD with the expected output of the coloring filter; in order to do that, we have to change the units, so to account for the fact that the input CPSD is expressed in Hz^-1.
%% Estimate the PSD % PSD estimation configuration plist psdPlist = plist(... 'scale', 'PSD', ... 'order', 1, ... 'win', 'BH92', ... 'navs', 25 ... ); % Estimate the PSD S_out_tm2_x = out_tm2_x.psd(psdPlist); % Plot the PSD and compare with the expected noise shape % We have to account for the unit of the input to the coloring filter GRScapactNoise_tm2_x_disc_resp.setYunits(sqrt(S_out_tm2_x.yunits)); iplot(sqrt(S_out_tm2_x), abs(GRScapactNoise_tm2_x_disc_resp));
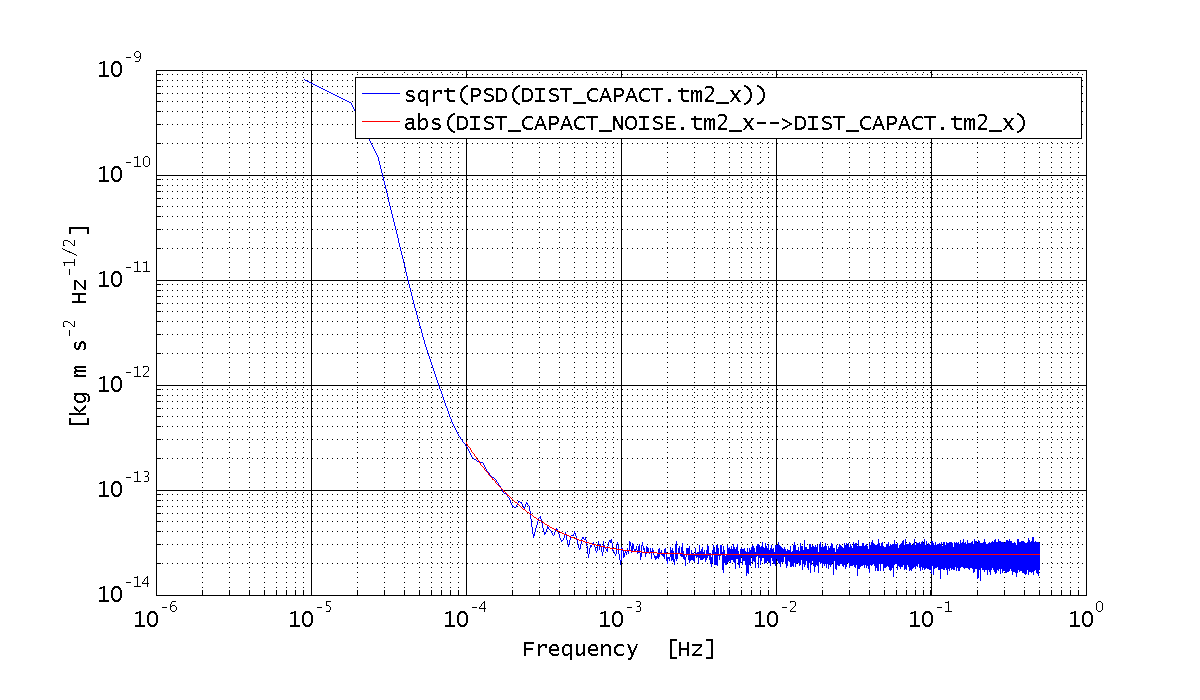
 |
Simulating harmonic oscillator noise | Simulating LPF noise |  |
©LTP Team