LTPDA Toolbox™ contents Simulating noise   Simulating capacitive actuation noise

Simulating harmonic oscillator noise

Basic system simulations

Let's begin with a simple example, namely the harmonic oscillator. The system can be built easily, specifying the values for the key parameters (mass, spring constant, viscous damping coefficient): 

  % Build a Harmonic Oscillator model
  % Physical parameters
  m     = .1;     % mass: 0.1 kg
  k     = 1e-2;   % spring constant: 1e-2 N / m
  vbeta = 1e-3;   % viscous damping coefficient: 1e-3 N s / m

  % Definition plist
  buildPlist = plist(...
              	'built-in', 'HARMONIC_OSC_1D', ...
                'm', m, ...
                'vbeta', vbeta, ...
                'k', k ...
                );

  % Build the ssm model
  harm_osc = ssm(buildPlist);
Now, a call to ssm/viewDetails is telling us that the system has two input blocks, namely 'COMMAND' and 'NOISE', representing respectively the force acting on the particle and the readout additive noise. Each of the input blocks has a single port, respectively 'COMMAND.force' and 'NOISE.readout', where data needs to have the proper physical units. 
  %% Look at the model details
  harm_osc.viewDetails
The system is continuous, i.e., it has a time-step of zero. We can verify this by inspecting its timestep property: 
  %% Check if the model is continuous
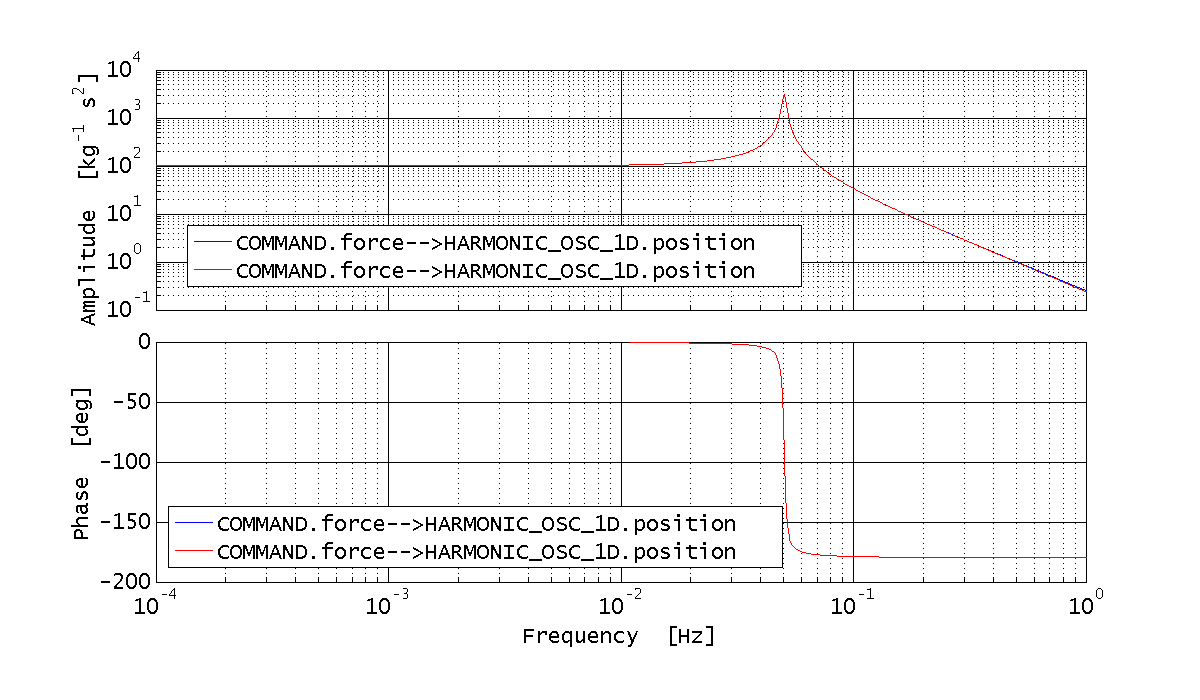
  harm_osc.timestep

Now we want to calculate the system transfer function of the input to the outputs, in order to estimate the effect of the sources. In order to do that, we can call the ssm/bode method, specifying the input port, the output port, and the frequency range. Here is an example, where we look at the response of the harmonic oscillator mass position to the application of an external force, in the range from 0.1 mHz t 1 Hz: 

  %% Calcolate the bode response from force to displacement for the continuous system
  forceBodePlist = plist(...
    'inputs', 'COMMAND.force', ...
    'outputs', 'HARMONIC_OSC_1D.position', ...
    'f', logspace(-4, 0, 1000) ... % from 0.1mHz to 1Hz
    );

  bode_output              = bode(harm_osc, forceBodePlist);
  harm_osc_cont_resp_force = bode_output.unpack();
NOTE: The output of bode is a matrix object. The single response we want (1 input to 1 output) is represented by the single ao inside the output matrix. So we unpack that single object from the matrix.

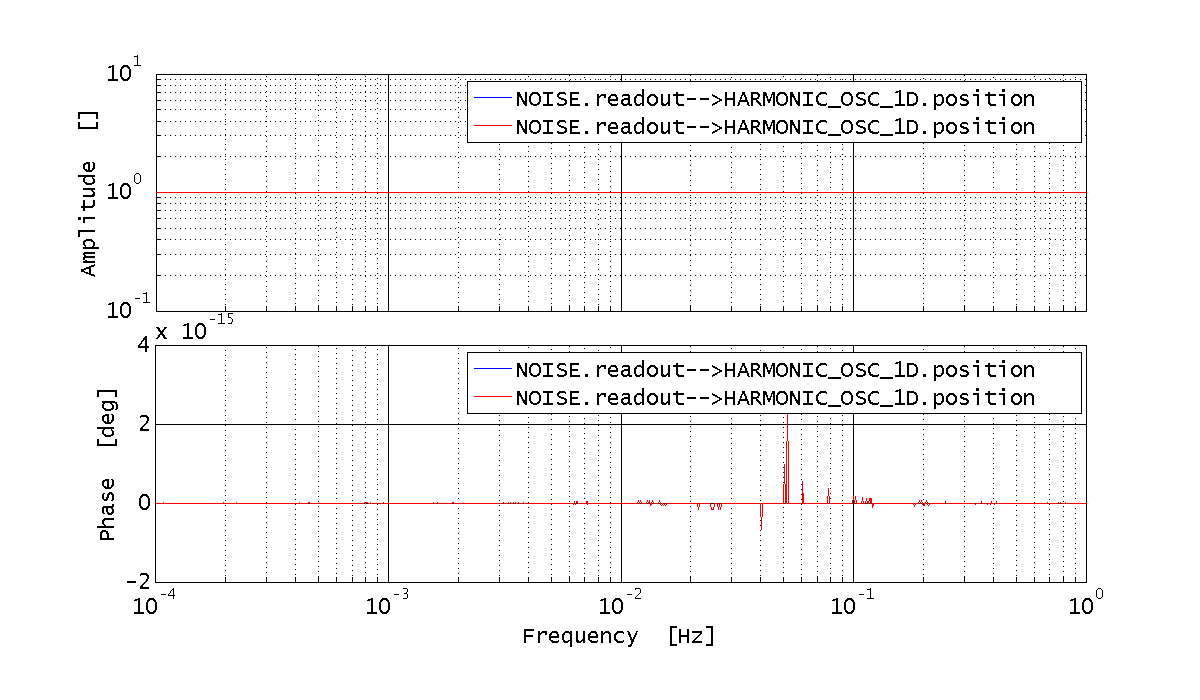
Similarly, we could look at the response of the harmonic oscillator mass position to the additive readout noise, in the range from 0.1 mHz t 1 Hz: 
  %% Calcolate the bode response from readout noise to displacement for the continuous system
  readoutBodePlist = plist(...
    'inputs', 'NOISE.readout', ...
    'outputs', 'HARMONIC_OSC_1D.position', ...
    'f', logspace(-4, 0, 1000) ... % from 0.1mHz to 1Hz
    );

  bode_output                = bode(harm_osc, readoutBodePlist);
  harm_osc_cont_resp_readout = bode_output.unpack();

Discretizing the system

In order to simulate the ssm models, we need to discretize them. This is done by setting the time-step to a non-zero value. 
  %% Discretize the system to be simulated at 10 Hz
  timestep = 0.1;
  harm_osc_discrete = harm_osc.modifyTimeStep(timestep);
The discretization of a continuous system is a delicate step, because it involves a change from s-domain to z-domain representation. In this case, we want to evaluate the impact of discretizing our harmonic oscillator at 10 Hz. To do so, we go ahead and calculate the transfer function of the discretized system, for both inputs, and compare them with the continuous ones. 
  % Calculate the bode response from force to displacement for the discrete system
  bode_output              = bode(harm_osc_discrete, forceBodePlist);
  harm_osc_disc_resp_force = bode_output.unpack();

  % Calculate the bode response from readout noise to displacement for the discrete system
  bode_output                = bode(harm_osc, readoutBodePlist);
  harm_osc_disc_resp_readout = bode_output.unpack();

  % Compare the transfer functions for the discrete and continuous case
  plot_plist = plist('linestyles', {'-', '--'});

  iplot(harm_osc_cont_resp_readout, harm_osc_disc_resp_readout, plot_plist);
  iplot(harm_osc_cont_resp_force, harm_osc_disc_resp_force, plot_plist);
We expect to see two plots similar to the following ones, showing that the effect of discretizing at this rate is very tiny, and as expected it impacts only at very high frequencies:





Simulating the system

Let's assume we only want to simulate the effect of the external force noise, so we simulate a single noise source. We can do that by specifying a single input name and a value for the CPSD of that noise source: 

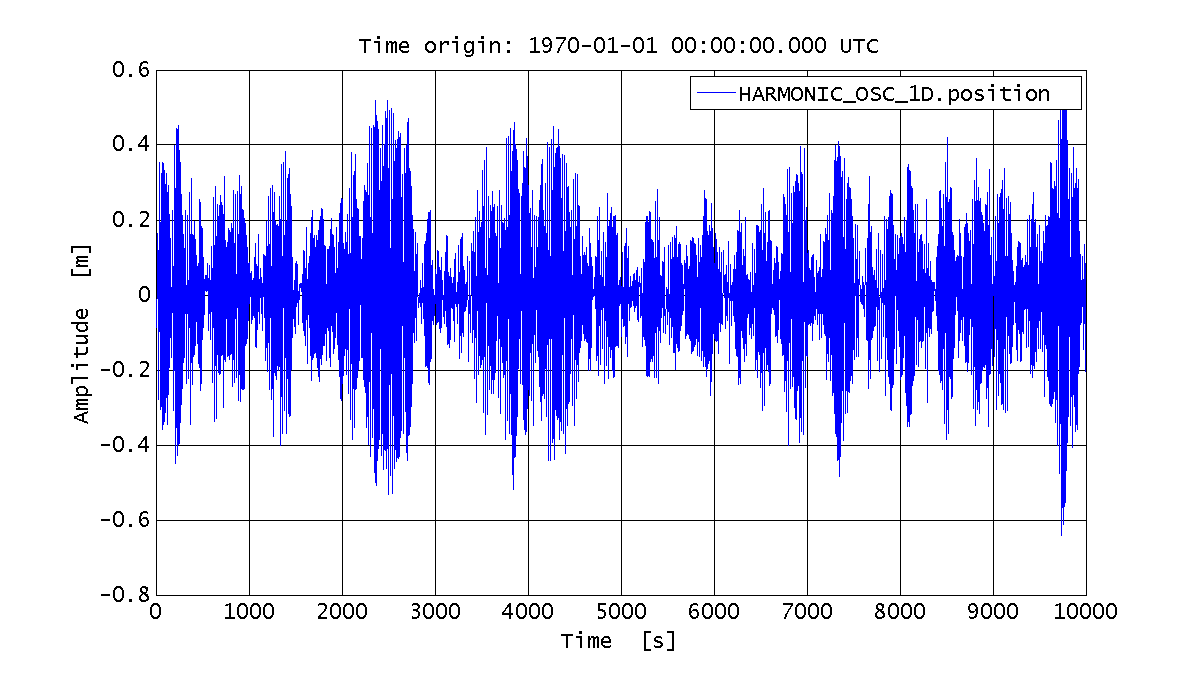
  %% Simulate the system behavior: only force noise
  % Simulation configuration plist
  simPlist_force = plist(...
    'CPSD Variable Names', 'COMMAND.force', ...
    'CPSD', 1e-6, ...
    'Return outputs', {'HARMONIC_OSC_1D.position'}, ...
    'Nsamples', 100000 ...
    );

  % Launch the simulation
  sim_output = harm_osc_discrete.simulate(simPlist_force);
  
  % Extract the AO with the postion data
  out_force = sim_output.unpack();
  
  % Plot the results
  iplot(out_force)
You should see a plot similar to the following one:



Similarly, let's assume we only want to simulate the effect of the readout noise, so we simulate a single noise source. We can do that by specifying a single input name and a value for the CPSD of that noise source: 

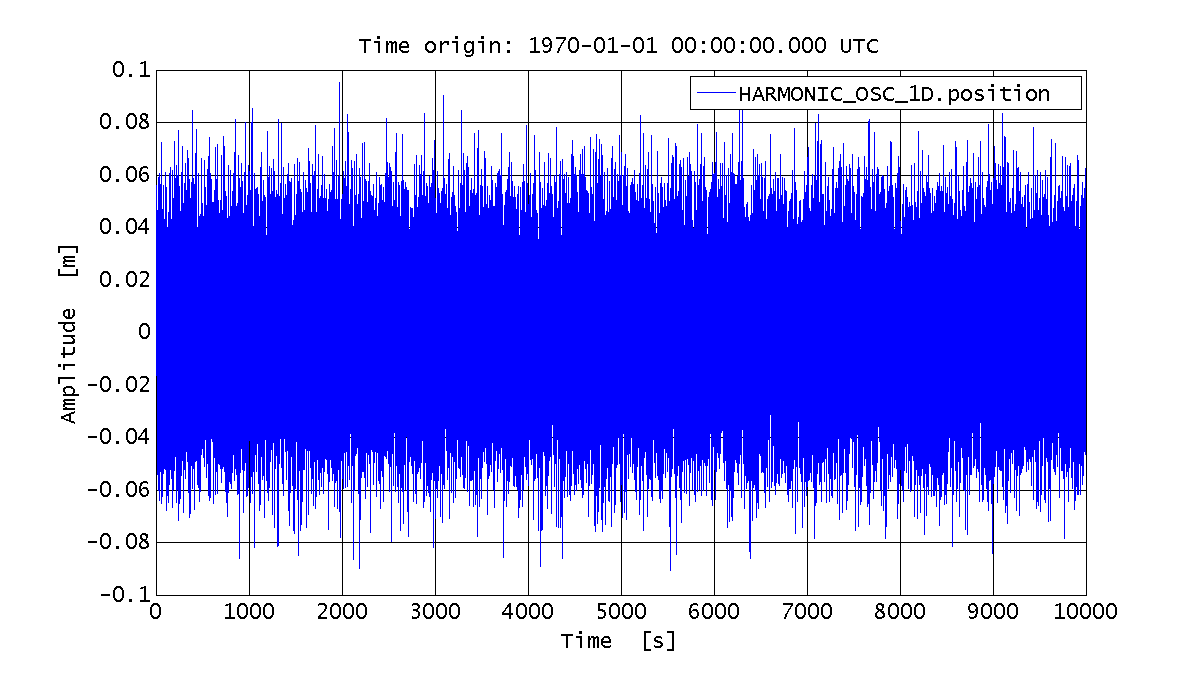
  %% Simulate the system behavior: only readout noise
  % Simulation configuration plist
  simPlist_readout = plist(...
    'CPSD Variable Names', 'NOISE.readout', ...
    'CPSD', 0.01, ...
    'Return outputs', {'HARMONIC_OSC_1D.position'}, ...
    'Nsamples', 100000 ...
    );

  % Launch the simulation
  sim_output = harm_osc_discrete.simulate(simPlist_readout);
  
  % Extract the AO with the postion data
  out_readout = sim_output.unpack();
  
  % Plot the results
  iplot(out_readout)
You should see a plot similar to the following one:



You can verify that by changing the CPSD quantity, the noise level changes accordingly.

Estimating the PSD

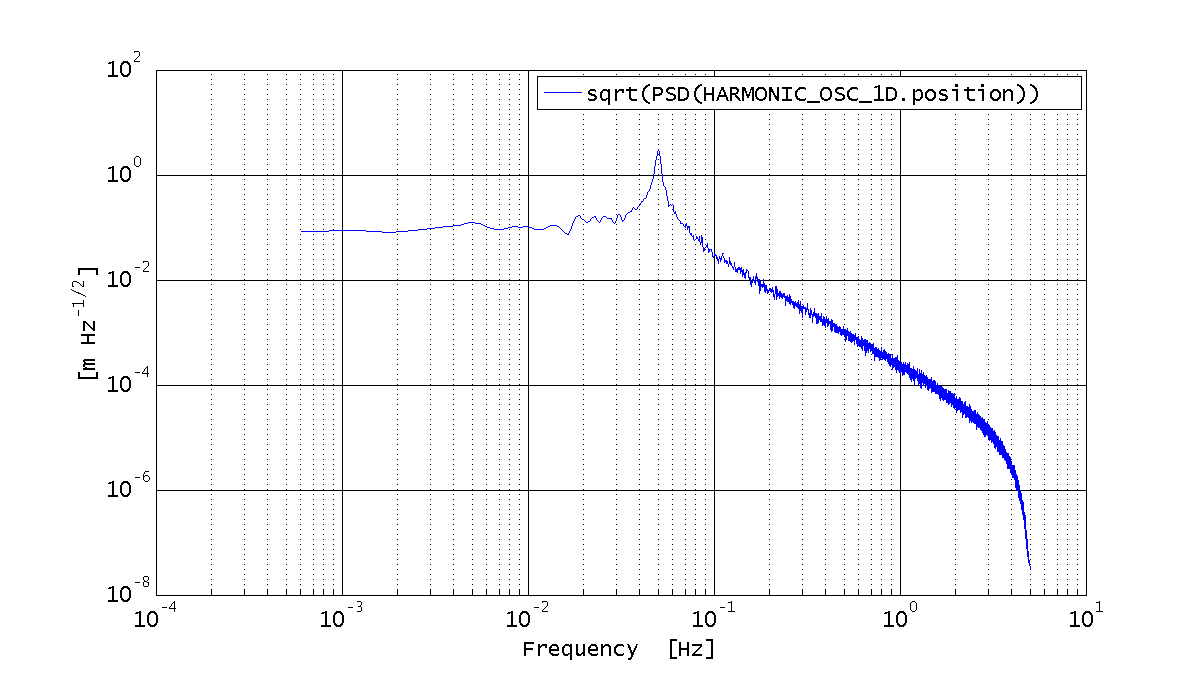
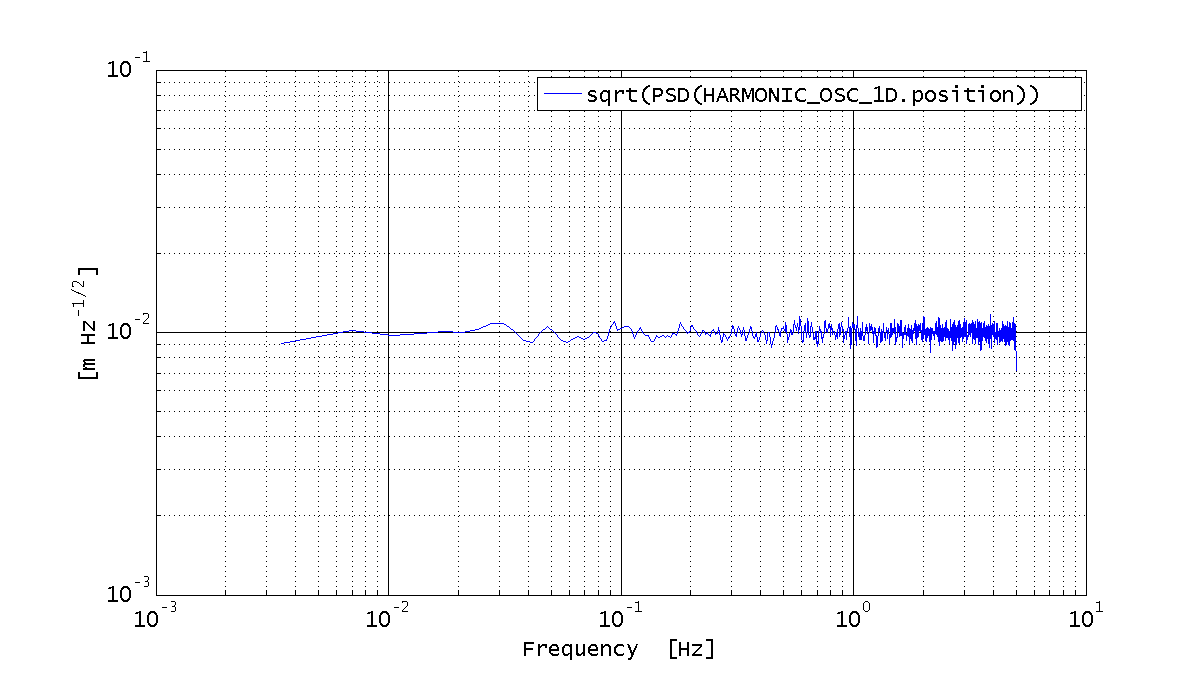
Eventually, we want to estimate the PSD of the displacement in the two cases. Just for curiosity, we change the number of averages in the two cases. 

  %% Estimate the PSD
  % PSD estimation configuration plist
  psdPlist = plist(...
    'scale', 'PSD', ...
    'order', 1, ...
    'win', 'BH92' ...
    );

  % Estimate the PSD
  S_out_force   = out_force.psd(psdPlist.pset('navs', 16));
  S_out_readout = out_readout.psd(psdPlist.pset('navs', 100));

  % Plot the ASD (sqrt(PSD))
  iplot(sqrt(S_out_readout));
  iplot(sqrt(S_out_force));

We expect to see two plots similar to the following ones:





Again, you can verify that by changing the CPSD quantity, the noise levels change accordingly.


Simulating noise  Simulating noise   Simulating capacitive actuation noise Simulating capacitive actuation noise

©LTP Team