LTPDA Toolbox™

Log-scale power spectral density estimates

Transfer function estimates

Description

The LTPDA method ao/tfe estimates the transfer function of time-series signals, included in the input aos following the Welch's averaged, modified periodogram method [1]. Data are windowed prior to the estimation of the spectra, by multiplying it with a spectral window object, and can be detrended by polinomial of time in order to reduce the impact of the border discontinuities. The window length is adjustable to shorter lenghts to reduce the spectral density uncertainties, and the percentage of subsequent window overlap can be adjusted as well.

Syntax

    
    b = tfe(a1,a2,pl)

a1 and a2 are the 2 aos containing the input time series to be evaluated, b is the output object and pl is an optional parameters list.

Parameters

The parameter list pl includes the following parameters:

'Nfft' - number of samples in each fft [default: length of input data] A string value containing the variable 'fs' can also be used, e.g., plist('Nfft', '2*fs')
'Win' - the window to be applied to the data to remove the discontinuities at edges of segments. [default: taken from user prefs].
The window is described by a string with its name and, only in the case of Kaiser window, the additional parameter 'psll'.
For instance: plist('Win', 'Kaiser', 'psll', 200).
'Olap' - segment percent overlap [default: -1, (taken from window function)]
'Order' - order of segment detrending
- -1 - no detrending
- 0 - subtract mean [default]
- 1 - subtract linear fit
- N - subtract fit of polynomial, order N
'Navs' - number of averages. If set, and if Nfft was set to 0 or -1, the number of points for each window will be calculated to match the request. [default: -1, not set]
'Times' - interval of time to evaluate the calculation on. If empty [default], it will take the whole section.

The length of the window is set by the value of the parameter 'Nfft', so that the window is actually rebuilt using only the key features of the window, i.e. the name and, for Kaiser windows, the PSLL.

As an alternative to setting the number of points 'Nfft' in each window, it's possible to ask for a given number of TFE estimates by setting the 'Navs' parameter, and the algorithm takes care of calculating the correct window length, according to the amount of overlap between subsequent segments.

If the user doesn't specify the value of a given parameter, the default value is used.

The function makes transfer functions estimates between the 2 input aos, and the output will contain the transfer function estimate from the first ao to the second.

Algorithm

The algorithm is based in standard MATLAB's tools, as the ones used by pwelch. The standard deviation of the mean is computed as

where

is the coherence function.

Example

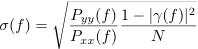
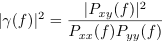
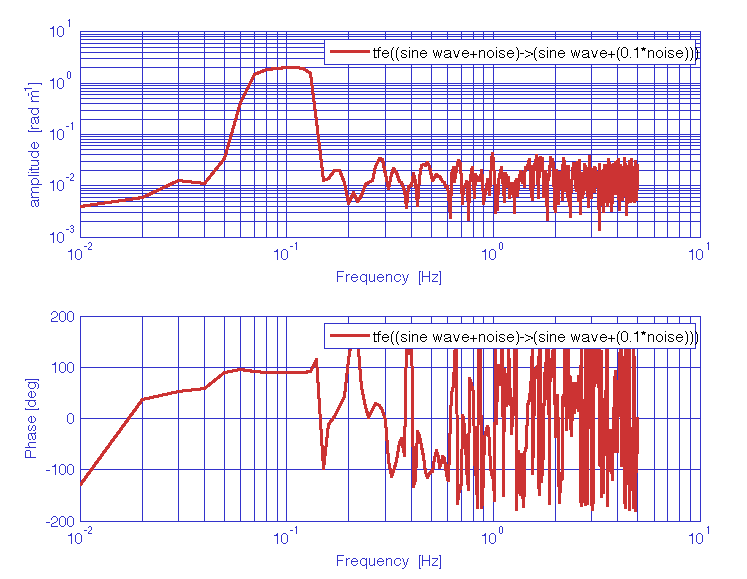
Evaluation of the transfer function between two time-series represented by: a low frequency sinewave signal superimposed to white noise, and a low frequency sinewave signal at the same frequency, phase shifted and with different amplitude, superimposed to white noise.

    
    % parameters
    nsecs = 1000;
    fs = 10;
    
    % create first signal AO
    x = ao(plist('waveform','sine wave','f',0.1,'A',1,'nsecs',nsecs,'fs',fs)) + ...
    ao(plist('waveform','noise','type','normal','nsecs',nsecs,'fs',fs));
    x.setYunits('m');
    
    % create second signal AO
    y = ao(plist('waveform','sine wave','f',0.1,'A',2,'nsecs',nsecs,'fs',fs,'phi',90)) + ...
    0.1*ao(plist('waveform','noise','type','normal','nsecs',nsecs,'fs',fs));
    y.setYunits('rad');
    
    % compute transfer function
    nfft = 1000;
    psll = 200;
    Txy = tfe(x,y,plist('win','Kaiser','psll',psll,'nfft',nfft));
    
    % plot
    iplot(Txy)

References

P.D. Welch, The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms, IEEE Trans. on Audio and Electroacoustics, Vol. 15, No. 2 (1967), pp. 70 - 73.

Cross coherence estimates

Log-scale power spectral density estimates