

| LTPDA Toolbox™ | contents |   |
The LTPDA method ao/lpsd estimates the power spectral density of time-series signals, included in the input aos following the LPSD algorithm [1]. Spectral density estimates are not evaluated at frequencies which are linear multiples of the minimum frequency resolution 1/T, where T is the window lenght, but on a logarithmic scale. The algorithm takes care of calculating the frequencies at which to evaluate the spectral estimate, aiming at minimizing the uncertainty in the estimate itself, and to recalculate a suitable window length for each frequency bin.
Data are windowed prior to the estimation of the spectrum, by multiplying it with a spectral window object, and can be detrended by polinomial of time in order to reduce the impact of the border discontinuities. Detrending is performed on each individual window. The user can choose the quantity being given in output among ASD (amplitude spectral density), PSD (power spectral density), AS (amplitude spectrum), and PS (power spectrum).
bs = lpsd(a1,a2,a3,...,pl)
bs = lpsd(as,pl)
bs = as.lpsd(pl)
a1 and a2 are the 2 aos containing the input time series to be evaluated, b is the output object and pl is an optional parameter list.
The parameter list pl includes the following parameters:
| If the user doesn't specify the value of a given parameter, the default value is used. |
The algorithm is implemented according to [1]. In order to
compute the standard deviation of the mean for each frequency bin, the averaging of the different segments is performed using Welford's
algorithm [2] which allows to compute mean and variance in one loop.
In the LPSD algorithm, the first frequencies bins are usually computed using a single segment containing all the data.
For these bins, the sample variance is set to Inf.
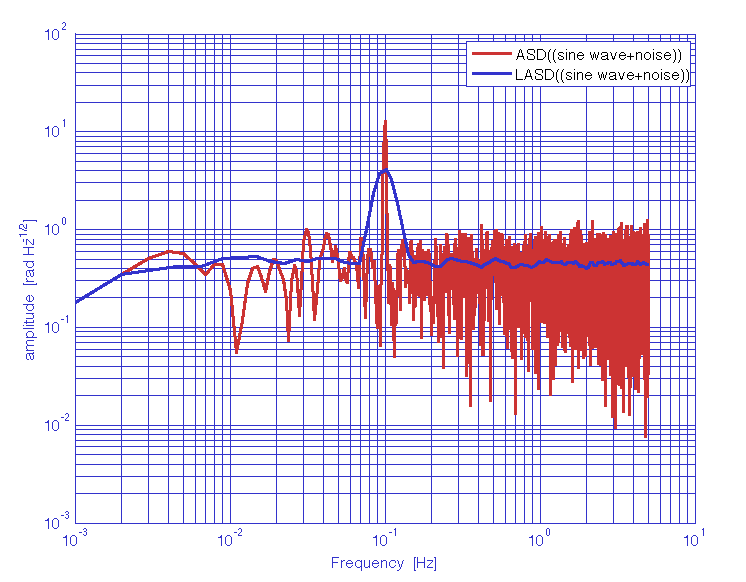
1. Evaluation of the ASD of a time-series represented by a low frequency sinewave signal, superimposed to white noise. Comparison of the effect of using standard Pwelch and LPSD on the estimate of the white noise level and on resolving the signal.
% Create input AO
x1 = ao(plist('waveform','sine wave','f',0.1,'A',1,'nsecs',1000,'fs',10,'yunits','rad'));
x2 = ao(plist('waveform','noise','type','normal','nsecs',1000,'fs',10,'yunits','rad'));
x = x1 + x2;
% Compute psd and lpsd
pl = plist('scale','ASD','order',-1,'win','Kaiser','psll',200);
y1 = psd(x, pl);
y2 = lpsd(x, pl);
% Compare
iplot(y1, y2)
 |
Transfer function estimates | Log-scale cross-spectral density estimates |  |
©LTP Team