Pole zero model representation

Creating a pole zero model

Let's build a pole zero model with the following characteristics:

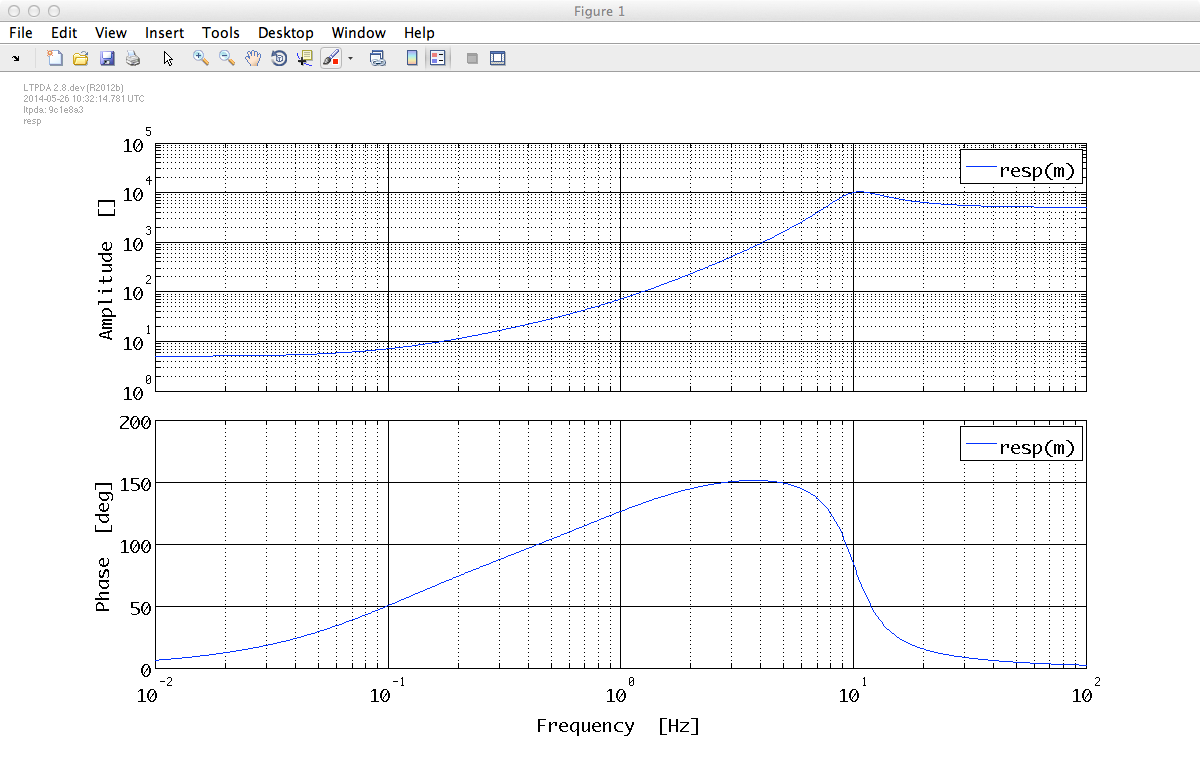
Our pole zero model has a pole at 10 Hz with a quality factor of Q = 2, and two zeros, one at 1 Hz, one at 0.1 Hz.

    m = pzmodel(5, [10 2], {1, 0.1})

We can easily obtain the response of this transfer function by using the pzmodel/resp method.

resp(m)

The result is the figure shown below.

Response of a pzmodel

The quality factor notation comes from the mechanical analogy of the harmonic oscillator. In short, we can classify systems in terms of Q as

Underdamped system (Q > 0.5): the system is described by a complex conjugate pair that represents an oscillating solution
Critically damped system (Q = 0.5): the system is described by two equal real poles. The system decays exponentially to equilibrium faster than in any other case.
Overdamped system (Q < 0.5): the system is described by two reals poles. The response is a exponential decay.

Create transfer function models in s domain

Partial fraction representation

$Partial fraction representation$