LTPDA Toolbox™ contents Estimate tranfser functions from simulated signals, compare with Bode estimates   Topic 5 - Introduction to system identification of LPF.

Simulate LPF with injected signals

We can, of course, do the same injections but with the full LPF model and with noise switched on.

In Topic 2 you already saw how to simulate an LPF model with all the noises switched on. If we combine that with the signal injections we've been doing in this topic, then a simulation with noise and injected signals can be done like this: 

  
      % Create a standard LPF model
      lpf = ssm(plist('built-in', 'LPF'));
      
      % Generate suitable covariance matrix for all inputs
      cov = lpf.generateCovariance;
      
      % Create some time-series analysis object to inject
      aSignal = ao(plist('tsfcn', '1e-7*sin(2*pi*0.005*t)', 'fs', 1/lpf.timestep, 'nsecs', 10000));       
      
      % Create the plist to configure simulate      
      sim_pl = plist('AOS', aSignal, 'AOS Variable Names', 'GUIDANCE.ifo_x1', ... 
                     'return outputs', {'DELAY_IFO.x1', 'DELAY_IFO.x12'}, ...
                     'CPSD variable names', cov.find('names'), ...
                     'CPSD', cov.find('cov'));
                    
      % Run the simulation      
      out = simulate(lpf, sim_pl);
We can then plot the two IFO outputs by doing: 
  
      % Unpack the outputs      
      [o1, o12] = unpack(out);
      
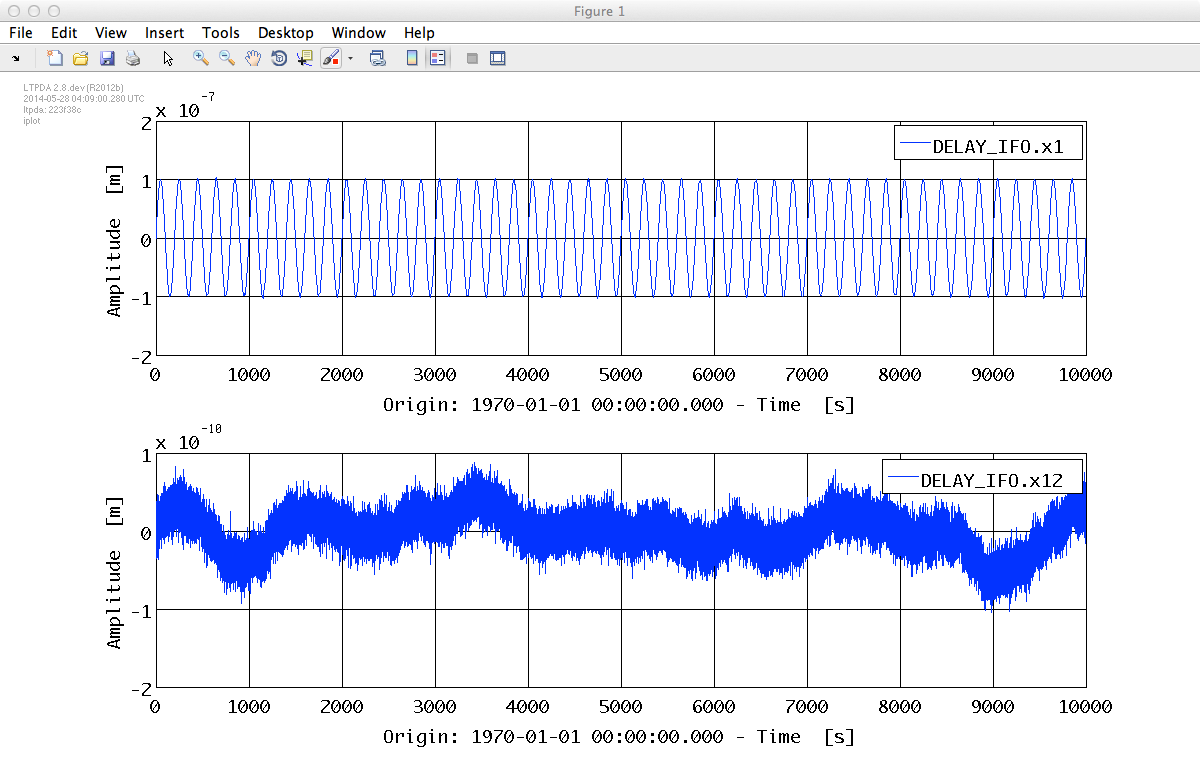
      % Plot on subplots      
      plot_pl = plist('arrangement', 'subplots');
      iplot(o1, o12, plot_pl);
This should result in a plot like this:

We can estimate the spectral densities of these two signals and we will should a signal at 5mHz: 
  
      % Create a PSD plist with 16 averages, linear segment-wise detrending       
      psd_pl = plist('navs', 16, 'order', 1, 'win', 'BH92');
      
      % Estimate PSDs      
      [o1_xx, o12_xx] = psd(o1, o12, psd_pl);
      
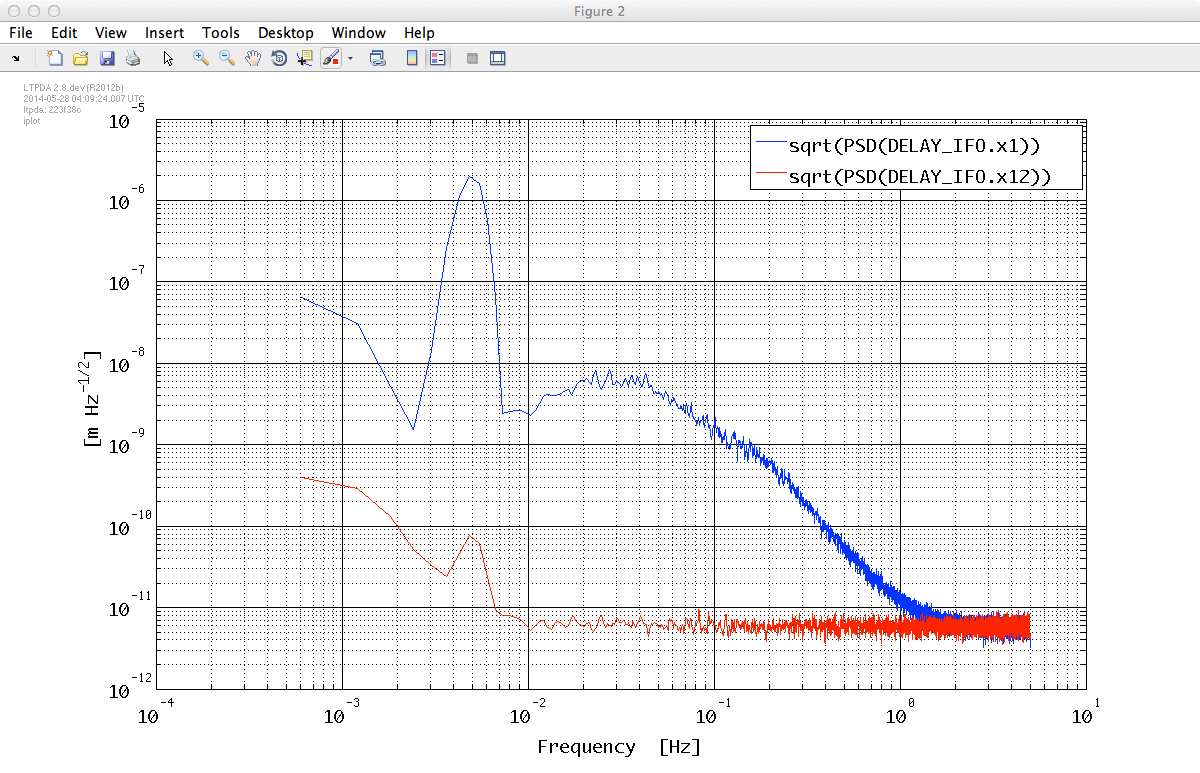
      % Plot the ASDs      
      iplot(sqrt(o1_xx), sqrt(o12_xx));
This should result in a plot like this:


Estimate tranfser functions from simulated signals, compare with Bode estimates  Estimate tranfser functions from simulated signals, compare with Bode estimates   Topic 5 - Introduction to system identification of LPF. Topic 5 - Introduction to system identification of LPF.

©LTP Team