

| LTPDA Toolbox™ | contents |   |
|
System identification in z-domain is performed with the function zDomainFit. It is based on a modeified version of the vector fitting algorithm that was adapted to fit in z-domain. Details on the core agorithm can be found in [1 - 3].
If you provide more than one AO as input, they will be fitted together with a common set of poles. Only frequency domain (fsdata) data can be fitted. Each non fsdata object is ignored. Input objects must have the same number of elements.
The function performs a fitting loop to automatically identify model order and parameters in z-domain. Output is a z-domain model expanded in partial fractions:
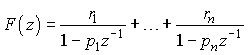
Each element of the partial fraction expansion can be seen as a miir filter. Therefore the complete expansion is simply a parallel filterbank of miir filters. Since the function can fit more than one input analysis object at a time with a common set of poles, output filterbank are embedded in a matrix (note that this characteristic will be probably changed becausse of the introduction of the collection class).
Identification loop stops when the stop condition is reached. Stop criterion is based on three different approaches:
The function can also perform a single loop without taking care of the stop conditions. This happens when 'AUTOSEARCH' parameter is set to 'OFF'.
In this example we fit a given frequency response to get a stable miir filter. For the meaning of any parameter please refer to ao and zDomainFit documentation pages.
pl = plist(...
'fsfcn', '(1e-3./(2.*pi.*1i.*f).^2 + 1e3./(0.001+2.*pi.*1i.*f) + 1e5.*(2.*pi.*1i.*f).^2).*1e-10',...
'f1', 1e-6,...
'f2', 5,...
'nf', 100);
a = ao(pl);
a.setName;
% Fit parameter list
pl_fit = plist('FS',10,...
'AutoSearch','on',...
'StartPolesOpt','clog',...
'maxiter',50,...
'minorder',15,...
'maxorder',30,...
'weightparam','abs',...
'CONDTYPE','MSE',...
'FITTOL',1e-2,...
'MSEVARTOL',1e-1,...
'Plot','on',...
'ForceStability','on');
% Do fit
mod = zDomainFit(a, pl_fit);
mod is a matrix object containing a filterbank object.
>> mod
---- matrix 1 ----
name: fit(a)
size: 1x1
01: filterbank | filterbank(fit(a)(fs=10.00, ntaps=2.00, a=[-1.19e+005 0], b=[1 0.0223]), fit(a)(fs=10.00, ntaps=2.00, a=[1.67e+005 0], b=[1 0.137]), fit(a)(fs=10.00, ntaps=2.00, a=[-5.41e+004 0], b=[1 0.348]), fit(a)(fs=10.00, ntaps=2.00, a=[1.15e+004 0], b=[1 0.603]), fit(a)(fs=10.00, ntaps=2.00, a=[-1.69e+005 0], b=[1 0.639]), fit(a)(fs=10.00, ntaps=2.00, a=[1.6e+005 0], b=[1 0.64]), fit(a)(fs=10.00, ntaps=2.00, a=[9.99e-009 0], b=[1 -1]), fit(a)(fs=10.00, ntaps=2.00, a=[-4.95e-010 0], b=[1 1]), fit(a)(fs=10.00, ntaps=2.00, a=[9.4e+003-i*3.7e+003 0], b=[1 -0.0528-i*0.0424]), fit(a)(fs=10.00, ntaps=2.00, a=[9.4e+003+i*3.7e+003 0], b=[1 -0.0528+i*0.0424]), fit(a)(fs=10.00, ntaps=2.00, a=[1.66e+003-i*1.45e+004 0], b=[1 0.0233-i*0.112]), fit(a)(fs=10.00, ntaps=2.00, a=[1.66e+003+i*1.45e+004 0], b=[1 0.0233+i*0.112]), fit(a)(fs=10.00, ntaps=2.00, a=[-1.67e+004+i*432 0], b=[1 0.171-i*0.14]), fit(a)(fs=10.00, ntaps=2.00, a=[-1.67e+004-i*432 0], b=[1 0.171+i*0.14]), fit(a)(fs=10.00, ntaps=2.00, a=[7.61e+003+i*7.36e+003 0], b=[1 0.378-i*0.112]), fit(a)(fs=10.00, ntaps=2.00, a=[7.61e+003-i*7.36e+003 0], b=[1 0.378+i*0.112]), fit(a)(fs=10.00, ntaps=2.00, a=[3.67e-015-i*4.61e-006 0], b=[1 -1-i*1.08e-010]), fit(a)(fs=10.00, ntaps=2.00, a=[3.67e-015+i*4.61e-006 0], b=[1 -1+i*1.08e-010]))
description:
UUID: 9274455a-68e8-4bf1-b1ad-db81551f3cd6
------------------
The filterbank object contains a parallel bank of 18 filters.
>> mod.objs
---- filterbank 1 ----
name: fit(a)
type: parallel
01: fit(a)(fs=10.00, ntaps=2.00, a=[-1.19e+005 0], b=[1 0.0223])
02: fit(a)(fs=10.00, ntaps=2.00, a=[1.67e+005 0], b=[1 0.137])
03: fit(a)(fs=10.00, ntaps=2.00, a=[-5.41e+004 0], b=[1 0.348])
04: fit(a)(fs=10.00, ntaps=2.00, a=[1.15e+004 0], b=[1 0.603])
05: fit(a)(fs=10.00, ntaps=2.00, a=[-1.69e+005 0], b=[1 0.639])
06: fit(a)(fs=10.00, ntaps=2.00, a=[1.6e+005 0], b=[1 0.64])
07: fit(a)(fs=10.00, ntaps=2.00, a=[9.99e-009 0], b=[1 -1])
08: fit(a)(fs=10.00, ntaps=2.00, a=[-4.95e-010 0], b=[1 1])
09: fit(a)(fs=10.00, ntaps=2.00, a=[9.4e+003-i*3.7e+003 0], b=[1 -0.0528-i*0.0424])
10: fit(a)(fs=10.00, ntaps=2.00, a=[9.4e+003+i*3.7e+003 0], b=[1 -0.0528+i*0.0424])
11: fit(a)(fs=10.00, ntaps=2.00, a=[1.66e+003-i*1.45e+004 0], b=[1 0.0233-i*0.112])
12: fit(a)(fs=10.00, ntaps=2.00, a=[1.66e+003+i*1.45e+004 0], b=[1 0.0233+i*0.112])
13: fit(a)(fs=10.00, ntaps=2.00, a=[-1.67e+004+i*432 0], b=[1 0.171-i*0.14])
14: fit(a)(fs=10.00, ntaps=2.00, a=[-1.67e+004-i*432 0], b=[1 0.171+i*0.14])
15: fit(a)(fs=10.00, ntaps=2.00, a=[7.61e+003+i*7.36e+003 0], b=[1 0.378-i*0.112])
16: fit(a)(fs=10.00, ntaps=2.00, a=[7.61e+003-i*7.36e+003 0], b=[1 0.378+i*0.112])
17: fit(a)(fs=10.00, ntaps=2.00, a=[3.67e-015-i*4.61e-006 0], b=[1 -1-i*1.08e-010])
18: fit(a)(fs=10.00, ntaps=2.00, a=[3.67e-015+i*4.61e-006 0], b=[1 -1+i*1.08e-010])
description:
UUID: 21af6960-61a8-4351-b504-e6f2b5e55b06
----------------------
Each object of the filterbank is a miir filter.
filt = mod.objs.filters.index(3)
------ miir/1 -------
b: [1 0.348484501572296]
histin: 0
version: $Id$
ntaps: 2
fs: 10
infile:
a: [-54055.7700068032 0]
histout: 0
iunits: [] [1x1 unit]
ounits: [] [1x1 unit]
hist: miir.hist [1x1 history]
procinfo: (empty-plist) [1x1 plist]
plotinfo: (empty-plist) [1x1 plist]
name: (fit(a)(3,1))(3)
description:
mdlfile:
UUID: 6e2a1cd8-f17d-4c9d-aea9-4d9a96e41e68
---------------------
 |
Iterative linear parameter estimation for multichannel systems - ssm system model in time domain | S-Domain Fit |  |
©LTP Team