

| LTPDA Toolbox™ | contents |   |
Determine the coefficients of a linear combination of noises and comapre with lscov
fs = 10; nsecs = 10; % Elements of the fit basis B1 = ao(plist('tsfcn', 'randn(size(t))', 'fs', fs, 'nsecs', nsecs, 'yunits', 'T')); B1.setName; B2 = ao(plist('tsfcn', 'randn(size(t))', 'fs', fs, 'nsecs', nsecs, 'yunits', 'T')); B2.setName; B3 = ao(plist('tsfcn', 'randn(size(t))', 'fs', fs, 'nsecs', nsecs, 'yunits', 'T')); B3.setName; % random additive noise n = ao(plist('tsfcn', 'randn(size(t))', 'fs', fs, 'nsecs', nsecs, 'yunits', 'm')); % coefficients of the linear combination c1 = ao(1,plist('yunits','m/T')); c1.setName; c2 = ao(2,plist('yunits','m/T')); c2.setName; c3 = ao(3,plist('yunits','m T^-1')); c3.setName; % build output of linear system y = c1*B1 + c2*B2 + c3*B3 + n; y.simplifyYunits;
% Get a fit with linlsqsvd
pobj1 = linlsqsvd(B1, B2, B3, y)
---- pest 1 ----
name: a1*B1+a2*B2+a3*B3
param names: {'a1', 'a2', 'a3'}
y: [0.81162366736073077;1.8907151217948008;3.0098623857384701]
dy: [0.091943725803872112;0.089863977231447567;0.097910574305897308]
yunits: [m T^(-1)][m T^(-1)][m T^(-1)]
pdf: []
cov: [3x3], ([0.00845364871469762 0.000268768332741779 0.000180072770333592;0.000268768332741779 0.00807553440385413 0.00125972375325089;0.000180072770333592 0.00125972375325089 0.00958648056091064])
corr: [3x3], ([1 0.0325289738130578 0.020003055941376;0.0325289738130578 1 0.143172656986983;0.020003055941376 0.143172656986983 1])
chain: []
chi2: 0.87276552675043451
dof: 97
models: B1/tsdata Ndata=[100x1], fs=10, nsecs=10, t0=1970-01-01 00:00:00.000 UTC, B2/tsdata Ndata=[100x1], fs=10, nsecs=10, t0=1970-01-01 00:00:00.000 UTC, B3/tsdata Ndata=[100x1], fs=10, nsecs=10, t0=1970-01-01 00:00:00.000 UTC
description:
UUID: b8628843-a1e8-4815-b69b-90efdadc16c2
----------------
% do linear combination: using eval yfit = pobj1.eval(B1, B2, B3); % Plot - compare data with fit result iplot(y, yfit)
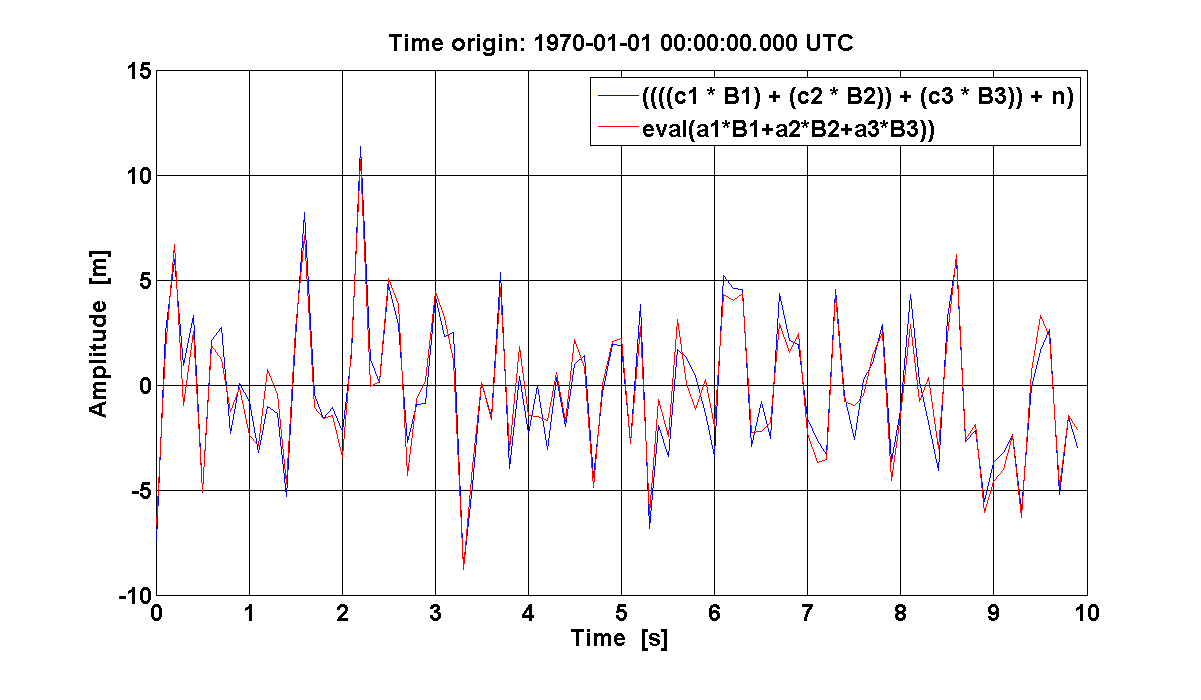
 |
Linear Parameter Estimation with Singular Value Decomposition | Linear least squares with singular value deconposition - multiple experiments |  |
©LTP Team