LTPDA Toolbox™

Sum of partial fractions representation

Transfer functions can be expressed as a quocient of polynomials

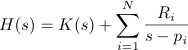
The constructor can be used in different ways

From poles and residues

The standard way is to input the coefficients of your filter. The constructor accepts as a optional properties the name

    >> par = parfrac([1 2+1i 2-1i], [6 1+3i 1-3i], [])
    ---- parfrac 1 ----
    model:    None
    res:      [1;2+i*1;2-i*1]
    poles:    [6;1+i*3;1-i*3]
    dir:      0
    pmul:     [1;1;1]
    iunits:   []
    ounits:   []
    -------------------

From partial XML file

You can input a XML file containing a transfer function model into the constructor

    >> par   = parfrac('datafile.xml')

From mat file

You can input a mat file containing a transfer function model into the constructor

    >> rat   = parfrac('datafile.mat')

From plist

All the properties of the filter can be specified in a plist and then passed to the constructor:

    >> pl = plist('iunits','m','ounits','V','res',[1 2+1i 2-1i],'poles',[6 1+3i 1-3i],...
    'name','filter_mame');
    >> par = parfrac(pl)
    ---- parfrac 1 ----
    model:    filter_mame
    res:      [1;2+i*1;2-i*1]
    poles:    [6;1+i*3;1-i*3]
    dir:      0
    pmul:     [1;1;1]
    iunits:   [m]
    ounits:   [V]
    -------------------

From repository

Rational transfer function can be obtained from the repository with the following syntax.

    >> rat   = rational('Hostname','localhost','Database','ltpda',...
    'ID',[],'CID',[],'Binary',yes)

Model helper GUI

Rational representation