LTPDA Toolbox™ contents Making a time-series AO   Saving and loading AOs

Basic math with AOs

Most of the basic math operations supported by MATLAB have been implemented as AO class methods. For example, suppose you want to add two AOs together, then you can do 

    a = ao(1);
    b = ao(2);
    c = a+b
    c.viewHistory

Note: the units of the two AOs for addition and subtraction must be the same. You can't add apples to oranges, but you can add dimensionless (empty units) to oranges.

Some of the standard operators can act as modifiers. For example, if you want to square an AO: 

    a = ao(2);
    a.^2

will do the job.

The operators follow MATLAB rules whenever possible. So if you want to add a single AO to a vector of AOs, you can. However, if you want to add two vectors of AOs together, the two vectors must contain the same number of AOs. For example, 

    a = [ao(1) ao(2) ao(3)];
    b = ao(4);
    c = a + b

will work fine and result in b being added to each element of a. However, 

    a = [ao(1) ao(2) ao(3)];
    b = [ao(4) ao(5)];
    c = a + b

will give an error.

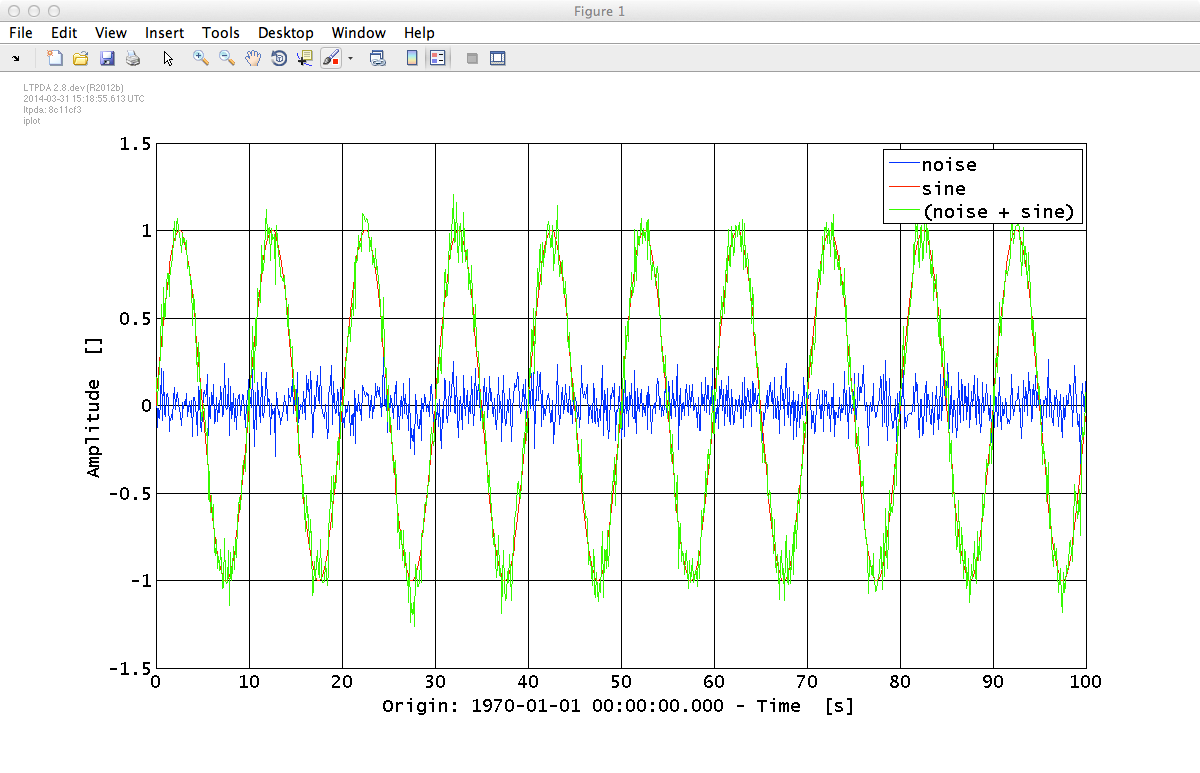
Addition operator on AOs by default acts on the y field, and it can be used to 'smartly' sum objects. For instance, time-series AOs can be added together provided they have the same time-base: 

    a = ao(plist('waveform', 'noise', 'fs', 10, 'nsecs', 100, ...
    'sigma', 0.1));
    b = ao(plist('waveform', 'sinewave', 'fs', 10, 'nsecs', 100, ...
    'A', 1, 'f', 0.1));
    c = a + b
    iplot(a, b, c)
Yielding a plot like the following: AO plus plot


Making a time-series AO  Making a time-series AO   Saving and loading AOs Saving and loading AOs

©LTP Team