

| LTPDA Toolbox™ | contents |   |
This exercise starts with the generation of simulated noise data.
% set output names
outNames = {...
'DELAY_IFO.x1' ... % o1 IFO
'DELAY_IFO.x12' ... % o12 IFO
'DFACS.sc_x', ... % Commanded force F_cmd_X
'DFACS.tm2_x' ... % Commanded force F_cmd_x2
};
% Define parameters and nominal values
params = {...
'FEEPS_XX', ... % FEEPs actuation gain
'CAPACT_TM2_XX', ... % Capacitive actuation gain
'IFO_X12X1', ... % The coupling of the x position of TM1 to the estimated x position of TM2
'EOM_TM1_STIFF_XX', ... % Total stiffness of TM1 along X
'EOM_TM2_STIFF_XX' ... % Total stiffness of TM2 along X
};
% set parameters values for the conversion to acceleration
FEEPS_XX = 1;
CAPACT_TM2_XX = 1;
IFO_X12X1 = 1e-4;
EOM_TM1_STIFF_XX = 1.3e-6;
EOM_TM2_STIFF_XX = 2.0e-6;
% actual values for the parameters
values = [...
FEEPS_XX, ...
CAPACT_TM2_XX, ...
IFO_X12X1, ...
EOM_TM1_STIFF_XX, ...
EOM_TM2_STIFF_XX];
% Create LPF SSM model
pl = plist('built-in', 'LPF', ...
'DIM', 1, ... % We use a one dimensional model
'CONTINUOUS', false, ... % The model is discrete
'param names', params, ... % Parameter names
'param values', values, ... % Parameter values
'VERSION', 'Best Case June 2011'); % Model version
LPF = ssm(pl);
% Create default noise covariance, assumes independent noise sources
cov = LPF.generateCovariance;
% Create a plist to configure the simulation
plsim = plist(...
'return outputs', outNames,...
'cpsd variable names', cov.find('names'), ...
'cpsd', cov.find('cov'), ...
'Nsamples', 1e6);
% Run the simulation
out = LPF.simulate(plsim);
% Unpack the signals from the simulation output matrix
[o1, o12, F_cmd_X, F_cmd_x2] = unpack(out);
Since the method for the conversion to acceleration uses a different naming convention for the parameters, it is convenient to set the convention mapping for the parameters.
Gdf = FEEPS_XX;
Gsus = CAPACT_TM2_XX;
SD1 = IFO_X12X1;
w1 = -1*EOM_TM1_STIFF_XX;
w2 = -1*EOM_TM2_STIFF_XX;
Note that in the method for the conversion to acceleration the stiffness is negative!
'ltp_ifo2acc' likes to work with SI units and in particular the force units have to be expressed in 'kg m s^(-2)'.
F_cmd_X.toSI;
F_cmd_x2.toSI;
Now we can set the parameter list for the conversion to acceleration.
pli2a = plist(...
'SD1', SD1,...
'Gdf', Gdf,...
'Gsus', Gsus,...
'w1', w1,...
'w2', w2,...
'OMS delay o1', 0.3, ...
'OMS delay oD', 0.3, ...
'Hdf', F_cmd_X*(-1),...
'Hsus', F_cmd_x2*(-1)...
);
Note the -1 multiplying the commanded forces, this is need because of a difference of convention between 'ssm' and 'ltp_ifo2acc' on the controllers outputs.
Now the conversion to equivalent residual acceleration of the interferometer displacement signals.
M = ltp_ifo2acc(o1, o12, pli2a); % M is a matrix object containing a1 and a12
Calculate the square root of the power spetral density in order to check the resuls.
plpsd = plist(...
'order', 1, ...
'SCALE', 'ASD' ...
);
Mxx = M.lpsd(plpsd);
Remove the first 6 samples (lowest frequencies bins) since they are corrupted by the window function.
plsp = plist(...
'samples', [7 inf] ...
);
Mxxs = Mxx.split(plsp);
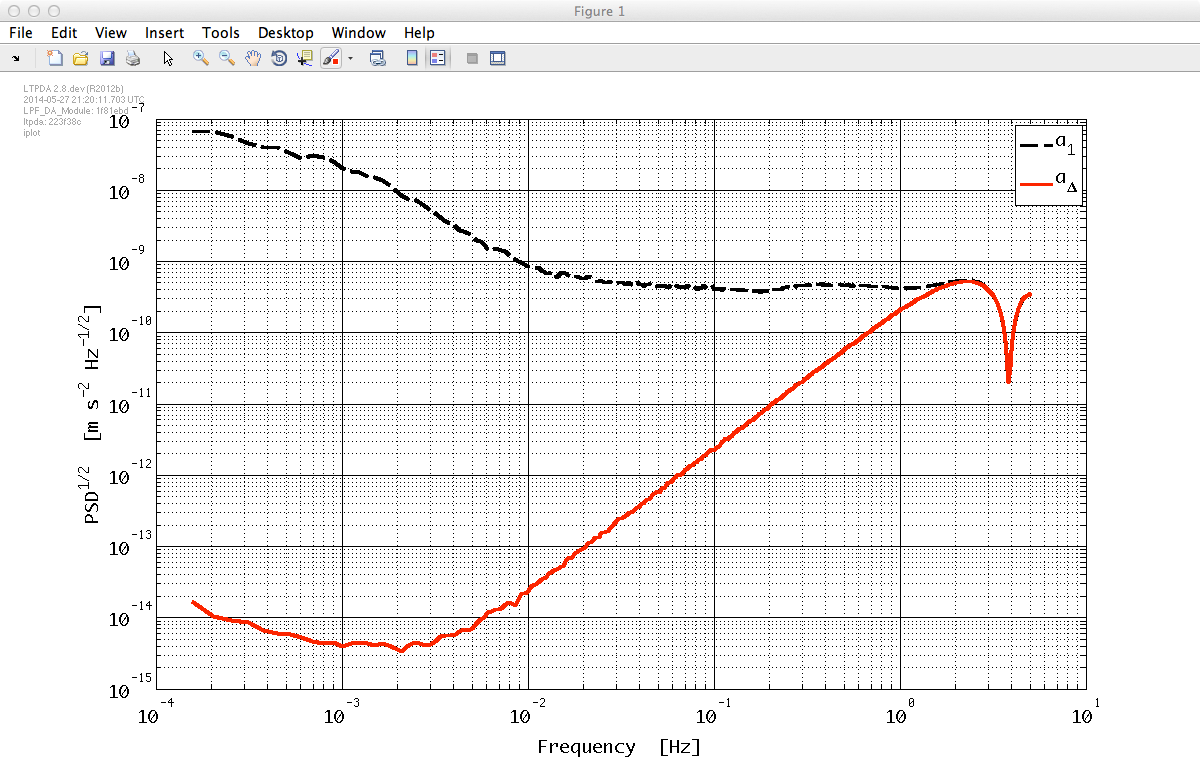
Finally, plot the result.
plplot = plist(...
'Linecolors', {'k', 'r'}, ...
'LineStyles', {'--', '-'}, ...
'LineWidths', {3, 3}, ...
'Legends', {'a_1', 'a_{\Delta}'}, ...
'XLABELS', {'All', 'Frequency'}, ...
'YLABELS', {'All', 'PSD^{1/2}'} ...
);
iplot(Mxxs, plplot)
 |
Tools for estimating the equivalent acceleration in LTPDA | Topic 4 - Simulating LPF with injected signals. |  |
©LTP Team